在新加坡,一道網紅題難倒新加坡教育部長首先,一道看上去相當簡單的小學數學題,因爲答案“多樣化”而刷爆網絡。
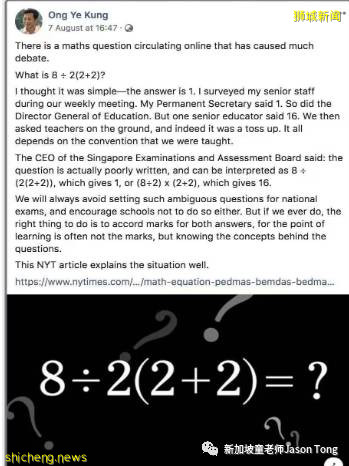
一道數學題驚動了新加坡教育部長王乙康,王部長在Facebook上說,“原本我以爲答案很簡單,就是1。我問了我的資深員工、國會秘書、教育署署長,他們的答案也是1。但資深教育工作者給出的答案卻是16。”
下面我們來看看這道題:
題目看起來很簡單
8 ÷ 2(2 + 2)= ?
這道題你的答案是?答對了麽?
一位教O水准的數學老師說,按照四則運算法則,這道題的正確答案應該是16。首先算括號裏的2+2=4,再按照從左到右的順序,先算除法8÷2=4,再算乘法4×4=16。但很多人,包括王乙康部長的算法卻是8÷(2(2+2))=1。王乙康部長提到,國家級的考試一般都會盡量避免出這類有歧義的題目。但是萬一真的出現這種題目。兩個答案都會被接受。
那麽,小小新加坡的數學水平高嗎?根據國際教育成就評測協會(IEA)進行的“國際數學和科學評測趨勢”(TIMSS)中,新加坡孩子的數學綜合成績遙遙領先,排名第一!!!
2015年TIMSS排名(四年級)
2015年TIMSS排名(八年級)
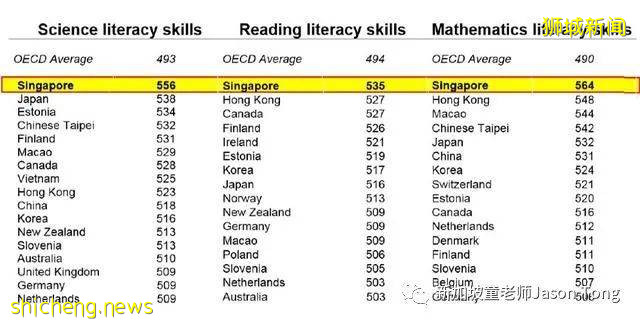
在世界最具影響力,由經濟合作與發展組織(OED)2016年最新的一輪“國際學生學術評估項目”(PISA)中,新加坡孩子的數學能力同樣位列全球第一,中國孩子位列第六。
被全球追捧的新加坡數學
到底好在哪裏?
其實,新加坡數學早已經風靡全球40多個國家。美國早就引入了新加坡數學,並且在美國大力在國內推廣與新加坡出版社聯合制作的SAP數學教材。英國早在4年前,就在全國小學采用新加坡數學教材。而法國也決定效法新加坡,在500多所學校引入新加披數學教材。
新加坡數學課本
無論是教材還是課堂設計,新加坡中小學的“數學模式”都是全世界效仿的對象。法國現已有超過500所學校引進新加坡教材,翻成法文,在課堂上推廣。目前,全世界已有超過40個國家及地區采用新加坡數學的課本進行教學,新加坡數學爲何如此受到“歡迎”?
新加坡數學的秘密無非是把傳統中國式注重練習、計算和結果的“抽象練習式”學習法,與西方注重過程、建構,將抽象概念具象化和尋找解決問題的“建構式”學習法進行融合形成了自己獨特的新加坡數學體系。
新加坡數學的法寶之一 “三步教學法”又叫 “CPA教學法”,這一理論也是新加坡數學的精髓。
這種教學方法,由美國心理學家Jerome Bruner在上個世紀60年代最先提出。他經過觀察發現,小孩子的學習,往往會經曆三個階段,分別是:Concrete 具象化、Pictorial 形象化、Abstract 抽象化。
下面來看一個簡單有效的例子,如何把抽象問題用圖形化方式來表達。
Model-Drawing,把抽象問題變圖形
國內外的很多小學基礎教育會通過互動的模式讓孩子能夠觸摸到物件,比如數蘋果或是掰手指頭等,然後將這個結果轉換成抽象的數字。“但是他們都忽略了一個步驟,就是將其圖片化,”新加坡國際學校小學部數學主任Frankie說,“增加這個步驟可以讓學生能夠有一個過渡的過程,更直觀地解讀問題。”
對此,新加坡開創了獨特的“Model-Drawing”學習方法。“很多人都會好奇這種方法是什麽,” Frankie說,“其實很簡單,就跟我之前說的那樣,Model-Drawing就是將抽象的問題變成方格的形式來解決,而美國人則把我們的這種方法稱爲Bar-Modeling。”
在新加坡數學的教學過程中,會逐漸出現一些Model-Drawing的方法,幫助學生一步步的解決問題。“我們在二年級就會引入了一些比較簡單的加減Model,三年級開始就會開始出現一些複合型的,如我們在初中階段會接觸到的告訴你兩數之和及兩數之差從而得出這兩個數字的未知數方程,”Frankie告訴記者,“很多比較具有難度的代數問題其實我們在小學階段都已經通過Model有所接觸了。”
他繼續道,“我們用這個方法學習數學並不是爲了能夠讓學生更早的接觸難度較高的內容,而是希望這樣的方法能夠讓他們對代數有一個基本的認知。——這其實是一種思維的模式,在有了這樣的思維方式和基本認知之後,代數本身就會變得簡單很多。”
如何Draw Models
說了那麽多,不如通過具體的題目來學一學Model-Drawing!
在Model中數字的大小通過方塊的長短來表示,並且大小一樣的方塊代表的是相同的數字。在進行Model的時候我們要注意幾點:
首先,在進行繪圖的時候一次只能針對一個信息進行處理;
其次,所有的題目的資料包括問題都要在Model中體現出來;
還有非常重要的一點,不一樣的數字要在繪圖中明顯的表現出來,並且,特別是兩個內容之中同樣的數字要排列整齊。
而Model本身通過題目的種類被簡單的分爲:“加減法”、“乘除法”、“比較”及“複合型”四種,接下來我們依次講一講如何用這幾種Model解決問題。
首先是“加減法模型”,該模型一般是以一個長條的形式來表現。
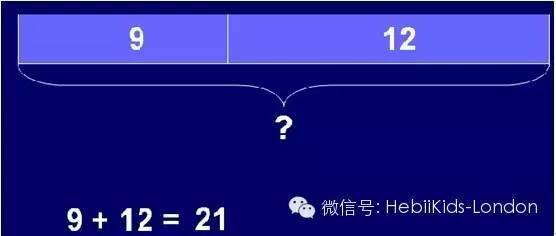
下面是一個簡單的“加減法模型”例題:
“Adam had 9 stickers. His brother gave hime another 12 stickers. How many stickers does Adamhave altogether?”
“很多家長都會誤以爲我們的這種方法是與中國的線段相類似的。其實不然,線段是將數字精確的標注出來,然後在上面進行計算得出結論,”Frankie說,“我們的這種Model不是一種類似代數這樣的計算方法,而是在計算過程中用到的工具。”
在Model上並不是精確的表現所要計算的數字的大小和比例,只是簡單的將其明顯的區分開。“我們通過將題目中的各種條件整合在一個圖片中宏觀地解讀問題,而後學生可以更快更清晰地解答問題。”
而新加坡數學中的乘除法模型則通過一個分爲若幹個部分的長條來體現:
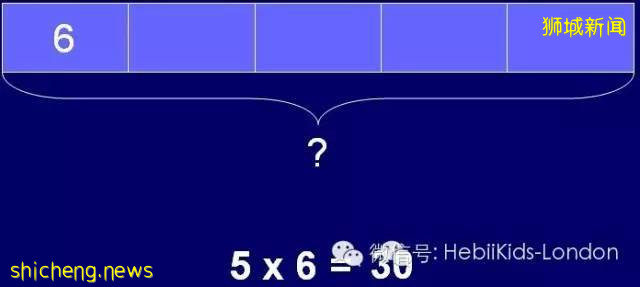
這是二年級學生的乘法題目:
“Fang Ting counted 5 nests on a tree. There were 6 birds in each nest. Howmany birds were there altogether?”
圖中的5個方格即題目中的“5 nests”,而6即每個鳥巢的小鳥的個數,問號的部分就是需要求解的內容。“在進行乘除法這樣會有很多方格的題目時,我們可以只標出一個方格的數字,在必要時可以將方格的數量用省略號表示,”Frankie提到,“有時候我們做除法的問題的時候,我們並不知道‘商’是什麽,這個時候我們就可以用問號或者省略號來代替。”
相對簡單的加減法和乘除法模型而言,比較型的模型相對更複雜,一般會有互相有比較的幾個長條組成。有這樣一個題目:
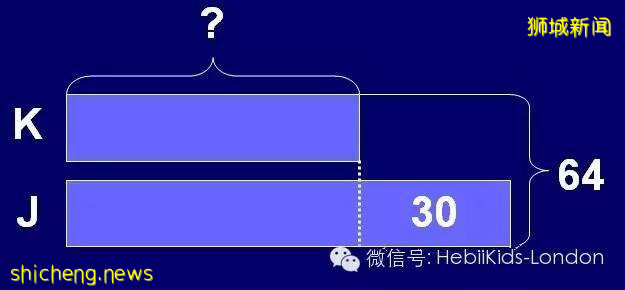
“Jane has 30 stamps more than Karen. They have a total of 64 stamps. How many stamps does Karen have?”
這其實是代數中非常基礎但很重要的問題,也就是“x + y = 64, x – y= 30”。而三四年級的學生,在掌握了比較型的模型後,就可以開始解決這類問題了。“做這樣問題的時候,我們教學的關鍵在于教會學生們把兩個不知道的問題慢慢變成一個問題,”Frankie開始講述教學的過程,“以這個問題爲例,我們可以從Model中非常直觀地看到K和J之間的比較,所以在第一步的時候就可以輕易的得出K+J的總數,從而得出結論。”
前幾種簡單的模型僅僅只是對Model-Drawing方法的入門,在解題中出現的較多的還是複合型模型,甚至可以說這是整個Model-Drawing教學中的“主力”。“並不是所有題目都是簡單的加減乘除,很可能一個問題之中會出現各種運算方式,”Frankie告訴記者,“所以複合型的模型是我們會著重教學的點。”
(部分文章選編自:外灘教育)