編者按:近日英國大數學家Atiyah仙逝,也許當今之世,在被封神(按照最高的標准,同時獲得Fields、Wolf、Abel獎三項大獎的數學家,稱之爲”神“大概不算太誇張)的大數學家中,要屬出生于1926年的法國數學家Serre最令人牽挂。
今天我們推出1985年2月14日(一個美妙的日子)由新加坡國立大學數學系莊志達、梁耀強兩位教授對他做的一個訪談。原文是英文(回複serre可以獲得PDF),發表于新加坡數學會的普及刊物Mathematical Medley(《數學萬象》,網址見:http://sms.math.nus.edu.sg/smsmedley/smsmedley.aspx)。有兩個中譯版,一個刊載于《數學傳播》(1987年)第2期,譯者呂素齡,一個刊載于《數學譯林》譯者張偉平、陳軍。這裏我們從台灣“數學知識”網站找到《數學傳播》版本的中文繁體版(http://episte.math.ntu.edu.tw/articles/mm/mm_11_2_06/index.html),轉換成簡體與大家分享,以下是正文。
——林開亮、孫志躍
● ● ●
作者 | 莊志達、梁耀強
譯者 | 呂素齡
塞爾(Jean-Pierre Serre) 1926年生于法國。在高等師範學校研讀數學。1954年,28歲時,他獲得國際數學協會的Fields獎,這是數學家的最高榮譽。兩年後,被任命爲法蘭西學院的代數和幾何學教授,在那兒連續大約15年他一直是最年輕的教授。1985年2月2日至15日,他訪問新加坡國立大學數學系,這次訪問是由“法—新學術交流計劃”資助。在訪新期間,塞爾教授就定義于有限體的代數曲線演講了兩次,就Ramanujan函數演講一次。此外,他提供一場兩小時的討論會,談論Faltings對Mordell猜測的證明,以及一場以虛二次域的類數爲內容的學術演講,題目是“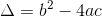
問:什麽促使你選擇數學作爲你一生的事業?
答:我記得我開始喜歡數學大約是七、八歲時。在高中時代,我常常做比我高年級的問題。那時我住在Nimes(尼姆,法國南部加爾省的省會——好玩的數學注)城供膳的寄宿處,跟比我年長的孩子生活在一起,他們經常欺負我。爲了討好他們,我常常替他們做數學作業。這跟其他任何的訓練方法一樣管用。
我母親是位藥劑師(我父親也是),她喜愛數學。在她還是 Montpellier(蒙彼利埃,法國南部城市——好玩的數學注) 大學藥學系的學生時,純爲了好玩,她選修了大一微積分,並通過了考試。她小心地保存了微積分課本(如果我沒記錯的話,那是Fabry 和Vogt 所寫的)。在我十四、五歲時,我常常翻閱、研讀這些書。這就是我學習導數、積分、級數等等的經過(我是用完全形式化的方法學習——也就是Euler 的方式:當時我並不喜歡,也不了解ε、δ)。那時,我並不知道當數學家可以過活。一直到很久之後,我才知道光是做數學也有人會給你薪水。我最先想當個高中老師:對我而言,那是很自然的。那時,我19歲,我通過考試進入高等師範學校。一旦進了高師,愈清楚看出來將來想當的並不是高中老師,而是數學研究者。
問:是否有其他的科目你曾經感興趣,譬如物理或化學?
答:物理學不怎麽有興趣,但化學倒是很有興趣。我說過,我雙親是藥劑師,因此他們有許多化學藥品和試管,在我十五、六歲時,做數學之暇也玩了不少化學實驗。我還讀了我父親的化學課本(我仍保存其中很有趣的一本,是Jacques Duclaux所寫的《Les Colloides》)。然而,在懂得更多的化學後,我對化學那些仿數學的外表感到失望:一長串的有機化合物,像甲烷CH4、乙烷C2H6等,全部看起來都有些相似。我想,假若你非得應付序列的話,還是甯願做數學中的序列!就這樣,我丟開化學——但不是全然放棄:我最後和一位化學家結婚。
問:在學數學的過程,你是否受到任何一位中學老師的影響?
答:我只有一位非常好的老師。這是在Nimes就讀高中的最後一年(1943-1944)。他被昵稱爲“大胡子”:那時留胡子人還不多。他頭腦很清楚、嚴密,他要求每一個式子和證明都要清楚寫下。爲了參加全國數學的“總競賽”,他嚴格訓練我。在那個競賽中,我終于獲得了首獎。
說到“總競賽”,在同一年(1944),我也在物理的競賽上試試我的身手。競試的問題全然是以我應該知道(事實不然)的某一個物理定律爲依據。幸運得很,我覺得只有一條式子符合那個定律。我就假設它是對的,並且用整六小時的時間解這個問題。我甚至認爲我會得獎。不幸我的式子是錯的,我什麽也沒有得到——本該如此!
問:在發現定理過程中,靈感有多重要?
答:我不知道“靈感”真正的意思是什麽。定理、理論以各種有趣的方式呈現。有時,你只是不滿意現有的證明,要找更好的,以便應用到不同的情境。我的一個典型的例子是,在處理Riemann-Roch 定理(大約1953)的時候,我把它看成Euler-Poincare 示性數(我那時並不知道Kodaira [小平邦彥] 與Spencer已經有同樣的想法)。我第一件工作是證明代數曲線的情形——一種大約一世紀前已經知道的例子!但我想要一種特別方式的證明,當我著手去找它的時候,我記得我花不到一、兩個鍾頭就從那兒推到二維的情況(這種情況剛由Kodaira完成)。六個月以後,一般的情形由Hirzebruch 證明,並且在他著名的教授就職演講發表。
通常,你不真的是硬碰硬的想要解決一個特定的問題。相反的,你心中有某些概念,你覺得這些觀念很有用,但你不真正知道它們爲什麽有用。所以,你四處瞧瞧,試著使用它們。這就像有一串鑰匙,你對著一些門試試看。
問:你是否經曆過,在你發現一個問題不能解決的當兒,把它擱置一些時候,突然靈光一閃,解答出現了?
答:是的,當然這種現象經常發生。例如,大約在1950年,我做同倫群(homotopy group)時,我自己確信,對給定的空間X,應該存在一個可縮的纖維空間(fibre space) E,他具有基底X;這樣的空間的確使我(應用Leray的方法)可以在同倫群和Eilenberg-MacLane的上同調群(cohomology group)做很多計算。但要如何找出它?我花了好幾個星期(非常長的時間,那時我還是……)才發現X上的所有的“環路”形成的空間具有我需要的所有的性質——只要我敢把它看成“纖維空間(fibre space)”,而我確是如此。在代數拓撲,這是環路空間(loop-space)方法的起始點,此後許多結果很快接連産生。
問:你通常是一次只做一個問題,或是同時做好幾個問題?
答:大約一次做一個問題,但不總是如此。而且我經常夜裏工作(在半睡眠狀態),事實上,那時你不需要寫下任何東西,而得以更集中心力,更爲容易改變主題。
問:物理學有很多意外的發現,像X 光、宇宙射線等等。你在數學是否有同樣的遭遇?
答:真正的意外很少。但有時你會很驚訝的發現,有些你爲某種目的而作的討論碰巧解決了不同方向的問題;無論如何,我們幾乎不能把這種情形稱爲“意外”。
問:代數幾何或數論的中心問題是什麽?
答:我無法回答這個問題。你知道,有些數學家有明確、長遠的計劃。例如,過去Grothendieck 在代數幾何有這種大計劃;目前Langlands 在表現論(與模函數、數論有關)也有這種大計劃。我從沒有這樣的大計劃,即使是小一點的也沒有,我只是做當下恰好感興趣的題目。(目前,我最有興趣的題目是計算定義于有限域的代數曲線的點的個數。這是一種應用數學:你使用你熟知的代數幾何和數論的工具……而你並沒有完全成功! )
問:你想代數幾何或數論在最近五年最大的發展是什麽?
答:這比較容易回答。Faltings對Mordell猜測和Tate猜測的證明,是我首先想到的。我也應提一提Gross-Zagier在二次數域類數(class number)的工作(這些工作是以過去Goldfeld的定理爲基礎),以及Mazur與Wiles使用模曲線(modular curve)探討Iwasawa理論的結果。(把模曲線和模函數應用到數論是非常有趣的:比如,你使用GL(2)去研究 GL(1)!顯然從那個方向會得出更多的東西——甚至有一天可能得到Riemann假設的證明!)
問:有些科學家在某個領域完成了決定性的成就,又很快轉到另一個領域。你在拓撲學作了三年後也改作其他的東西。這是怎麽回事?
答:這是連續的過程,不是突然的改變,1952年,我寫完有關同倫群的博士論文後,就到普林斯頓,在那兒演講這個題目(及其續篇“C-理論”),同時參加著名的Artin 與Tate 合辦的類域論(class field theory) 的研討會。然後,我回到巴黎,Cartan 的研討會正在討論多複變函數和Stein 流形。總結是Cartan-Oka 最近的結果如果使用上同調群和層論(sheaf) 的方法來討論,會更有效率,並且更簡單。這很讓人吃驚,我在這個題目上花了短暫的時間,把Cartan 定理應用到Stein 的流形。然而,多複變很有趣的一部分是研究射影簇(projective varieties)(相對于仿射(affine) 簇——它對幾何而言是有些缺陷);所以,我開始使用層論來探討這些複射影簇:這是我爲何在1953年卷入以Riemann-Roch 定理爲中心的各種問題。但是複射影簇是代數簇(周炜良的定理),因此使用解析函數來研究這些代數的材料是有點兒不自然,因爲這些解析函數可能有許多本質奇異點(essential singularities)。顯然,有理函數應該夠用了——事實上也是如此。這使我(大約1954年)走進了定義在任何代數閉域(algebraically closed field) 之上的抽象代數幾何。但爲何要假設體是代數封閉?有限域會更有趣,如Weil 猜測以及諸如其他的一些問題。從這兒到數論的領域是很自然的轉變……這多少是我所遵循的路線。
另一個工作方向來自我和Armand Borel 的合作。他教我許多李群(Lie group) 的知識,他認識李群的方式簡直與衆不同。這些群和拓撲、代數幾何、數論……的關聯把我迷住了。且讓我爲你舉個例(那是我在1968年左右才了解的)。
考慮SL2(R)最簡單的一個離散子群,那就是Γ=SL2(Z) 。我們可以計算它的Euler-Poincare示性數χ(Γ),它是-1/12(不是整數,因爲Γ有torsion)。現在正巧是黎曼Zeta函數在點ξ=-1的值ξ(-1)(Euler已經知道的結果)。而且這不是巧合!它可以推廣到任何全實的數體K,並且可以用來研究ξK(-1)的分母。(後來發現,借著使用模函數,可以得到更好的結果)這樣的問題不光是群論,不光是拓撲,也不光是數論,它們只能叫做數學。
問:數學這麽多不同的領域達成統合的展望如何?
答:我要說這種境界已經達到了。在前面我已經舉了一個典型的例子,其中李群、數論等已經合而爲一,且無法彼此分離。讓我舉另一個這樣的例子(很容易再舉更多的例子)。
有一個探討四維緊致可微流形的漂亮定理,最近才由S. Donaldson 加以證明。它說,這種流形在二維上同調群的二次形受到很強的限制:若它是正定的,則它是平方合。而且證明的要點是去建立某些輔助的共邊流形作爲一些偏微分方程(當然!是非線性的)的解集合!這是把分析應用到微分拓撲的一種全新應用。而它更引人注目的是,如果把可微的假設去掉,情形變得完全不同:由M. Freedman 定理,則二維上同調群的二次型幾乎可以是任何東西。
問:我們要如何才能趕得上數學知識的爆炸?
答:你實在不必去追趕。當你對某一特別的問題有興趣時,你很難發現現成的東西跟你有任何關聯,而如果有某些東西確實跟你相關,你會學得很快,因爲你知道要如何應用它。定期地看數學評論(特別是關于數論、群論等的集刊)也是個好習慣。你也可以從你的朋友那兒學到不少東西,在黑板講給你聽的證明是要比自己念的容易得多。
更重要的問題是關于所謂的“大定理”,它們一方面非常有用;一方面又長得無法檢驗(除非你爲它們耗下一生相當多的時光)。一個典型的例子就是Feit-Thompson 定理:秩爲奇數的群是可解群。(Chevally 曾嘗試以它來作爲討論會的主題,把它的證明予以完整的討論。兩年之後,他終于放棄了。)萬一我們要使用這樣的定理時該如何?信任地接受它們?大概吧!但這不是非常令人舒服的情況。
我也對某些東西感到不安,主要是在微分拓撲方面,作者畫了一個複雜的二維圖形,要求你接受它是五維或是更高維的證明,只有專家才“看”得出來這樣的證明是對或錯——假若你稱它是一個證明的話。
問:你認爲電腦將來對數學發展的沖擊如何?
答:電腦對數學某些部分已經有不少好的影響。例如在數論,人們以各種方式使用電腦。當然,首先是提供猜測或問題。此外,也用來檢驗一般性定理的特例——它對發現可能的錯誤很有幫助。
要進行大型的分類時也有很大助益(例如,當你必須檢驗106或107種情況時)。著名的例子是四色定理的證明。不過這兒有一個問題,跟Feit-Thomapson定理的問題有點類似。這樣的證明無法用手檢驗,你需要一台電腦(以及非常巧妙的程式)。這也不怎麽令人舒服。
問:我們要如何才能鼓勵年輕人念數學,特別是在中小學裏?
答:我在這方面有個理論是起先最好不要鼓勵年輕人學數學,因爲並不需要太多的數學家。但是,往後他們仍堅持學數學,就要確實鼓勵他們、幫助他們。
就中學生來說,最主要的一點是讓他們了解數學的的確確存在著,它不是死的(他們有一種傾向,相信只有物理或生物有未解決的問題)。傳統數學教法的缺點是,老師從不提及這些尚未解決的問題。真可惜!例如,在數論方面,有許多問題是十多歲的小孩就可以了解的:費馬定理當然是,Goldbach定理也是,以及無限多n2+1形式的質數存在性。而我們不妨只敘述定理而不證明它們(例如Dirichlet關于等差數列中的質數數目的定理)。
問:你認爲數學在近三十年的發展要比過去三十年的發展來得快嗎?
答:我不能確定是否如此。風格是不相同的。在五、六十年代,經常強調一般性的方法:廣義函數、上同調等等。這些方法非常成功,但現在人們做更具體的問題(通常,有些相當古老的問題:例如在複三維射影空間中代數曲線的分類!)他們應用過去發展完成的工具,這是相當好的。(而且他們也産生新的工具:微局部分析、超流形、相交上同調……)。
問:鑒于數學知識的爆炸,你想一位研究生能夠在四、五、六年間吸收大量的數學,然後立刻展開原創性的工作嗎?
答:爲什麽不能?就一個特定的問題,通常你不需要懂得很多。此外,非常簡單的概念經常就能解決問題。
有些定理被簡化了,有些只是被遺忘了。譬如,在1949年我記得我變得很沮喪,因爲當時每期的《數學年刊》(Annals of Mathematics) 都有一篇拓撲學的論文,並且一篇比一篇難。但現在沒有人再看這些論文了,它們被遺忘了(也該當如此:我不認爲它們包含有任何深度的東西……)。遺忘是非常健康的。
雖然如此,由于要使用繁重的技巧,有些題目真的還是比其他的題目需要更多的訓練。代數幾何就是這樣的例子,表示論也是。
無論如何,我們顯然不會說:“我要開始做代數幾何了”或其它類似的話。對某些人而言,僅是跟隨討論會,讀東西,問自已問題;而後學習做問題所需要的知識就夠了。
問:換句話說,我們應當首先針對一個問題,然後學習這個問題所需要的各種工具。
答:有點類似這樣子。但因爲我知道對自己都不能有好的建議,我也不可能給別人好的建議。我並沒有一副萬應靈丹。
問:你提到被遺忘的論文。已出版的論文你認爲有多少百分比不會被淘汰?
答:我相信是非零的百分比。畢竟,我們仍然充滿喜悅地閱讀Hurwitz、Eisenstein,或甚至Gauss的論文。
問:你想你將來會對數學史有興趣嗎?
答:我現在就有興趣了。但這可不容易;例如,我沒有拉丁或希臘文的語文能力。而且我有自知之明,叫我寫數學史的論文比寫數學論文還要花時間。然而曆史是非常有趣的,它把事情看得更透徹。
問:你相信有限單群的分類嗎?
答:多少相信——也比較傾向相信。假使有新的離散單群被發現,我會很高興,但我擔心不會發生。
更鄭重的說,這個分類定理是了不起的事情。我們現在只需利用通過有限單群的清單就可以檢驗許多性質。(典型的例子:對n≥4,n重可遷群的分類)。
問:在有限單群分類後,你想到的新開端是什麽?
答:你是暗指某些有限群理論家在分類完成後會變得沮喪的這件事實;有人說(或者我聽到的):“在那之後,就沒有什麽事可做了。”我發覺這是很可笑的!當然有許多事要做!首先,簡化證明(就是Gorenstein說的“修正主義”)。還有尋找它在數學其他部分的應用;例如,已經有很奇妙的發現把Griess-Fischer 怪物群與模函數聯系起來。
這就像在問Faltings 對Mordell 猜測的證明是否扼殺了曲線上有理點的理論。不會的!這只是一個開始。許多問題仍然未解。
(有時候,也真的有些理論被消滅了。一個有名的例子是Hilbert的第五個問題:證明每一個局部歐氏的拓撲群是一個李群。當我是一位年輕拓撲學家時,那是我確實想去解的問題——但我一無所獲。解出這個問題是Gleason、Montgomery 與Zippin,而他們的解只是扼殺了這個問題。在這個方向還有什麽其他的問題呢?我只能想到一個問題:p-進整數群能有效的作用在流形上嗎?這似乎很難——但就我所知,這個解應該沒有其他任何的應用了)。
問:但我們會假設大部分的數學問題都像這樣,即問題本身可能佷難且富挑戰性,不過當它們解決了以後就變得沒用了。事實上,很少問題像黎曼猜測一樣,甚至在未解之前,人們已經知道它的許多影響。
答:是的,黎曼猜測是非常好的例子;它導出很多東西(包括純粹數字的不等式,譬如在數體的判別式)。但還有其他類似的例子:Hironaka [廣中平佑] 的奇異點消去定理算是一個;當然還有前面討論到的有限單群。有時,用來證明的方法有許多應用:我確信這種現象會在Faltings 定理發生。有時,問題真的沒預計會有應用産生;他們是對現存定理的一種檢驗,迫使我們看得更深入。
問:你仍會回到拓撲方面的問題嗎?
答:不會的,我沒有繼續接觸最近的技巧,而且我不清楚圓的同倫群,πn+k(Sn) ,最新的計算值(我猜大約已算到k=40或50。我一向只知道k =10左右的結果)。
但我仍然以更廣義的方式使用拓撲學的觀念,像上同調、障礙論、Stiefel-Whitney 示性類等。
問:Bourbaki 在數學方面所造成的影響如何?
答:非常好!我知道把每件壞事都歸罪Bourbaki(譬如“新數學”是一種時尚,但這是不公平的。Bourbaki是不應負責任的。人們只是誤用Bourbaki 的書,這些書從沒打算作大學教科書,更不必說高中了。
問:或許應該有一些警告的訊息。
答:這樣的警告訊息Bourbaki 的確提過:那就是Bourbaki 討論會。這個討論會一點都不像書本那麽正式;它包括各類的數學,甚至某些物理。假使你把討論會和書合起來,你會獲得更均衡的看法。
問:你是否看到Bourbaki 對數學的影響已減退?
答:目前的影響有別于過去的。四十年前,Bourbaki 想作的論點是證明把數學予以組織化、系統化的闡述是可能的。現在這個想法已經做到了,而且Bourbaki也贏了。結果是,他們的書現在只剩下技術層次的意義;問題只是它們是否把主題好好的解說。有時它們做到了(有一本探討“根系”的已經成爲這一領域的標准參考資料);有時它們沒有做到(我不想舉例,這太牽涉到品味問題)。
問:談到品味,你能否談談那一類型的書或論文,你最喜歡?
答:嚴謹而不拘形式的!那是理想典型,就像是用來演講的。在像Atiyah 或Milnor 等少許作者,你可以看到這種令人愉快的溶合。但這種境界實在很難達到。例如,我發現很多法國人(包括我自己)有點太形式化了,而有些俄國人又有點太不嚴謹了……
還有一點我想提的是論文應多包含些評注、未解問題等等。通常,這些比定理的證明更有意思。哎!大多數的人卻害怕承認他們不知道某些問題的答案,連帶地他們就避免提問題,即使是非常自然的問題。多遺憾啊!對我自己而言,我是以說“我不懂”爲榮。
10年前的塞爾
編者補充:Serre有不少著作也譯成中文,例如:
他最近出版的一本新書是有限群的導引,見
• end •
傳播數學,普及大衆
長按識別二維碼關注我們
歡迎把我們推薦給你身邊的朋友
▼
點個“好看”再走呗▼▼▼




