時下朋友圈最熱的話題,無疑是各路高考喜報了。
不過對咱們平台的大多數家長來說,娃還有好多好多年才考大學,臨淵羨魚不如退而結網,從小規劃好孩子的學習,紮實掌握每門學科知識,讓孩子以後有更大的學校選擇權才是正道。
向上的道路愈發擁擠,但依然是天道酬勤的!
今天就來和大家講講數學,講講逃逃刷了很多年的新加坡數學。
還是從一道上了熱搜、被吐槽的高考數學題講起,
從計算量來看,這基本上就是一道小學題,不過有兩個“陷阱”:
1. 文字很多,讓人咋一看誤以爲是要算維納斯的身高,其實仔細讀題你會發現,它跟維納斯身高半毛錢關系都沒有;
2. 前面說黃金分割比例時,用的距離是“頭頂到咽喉”、“肚臍到足底”,後面給出的條件卻是 “頭頂到脖子下端”是26cm,和“腿長”是105cm,並不能完全對應上,所以很可能要用到假設和範圍估算。
解法其實很簡單,畫兩個圖就能搞定:
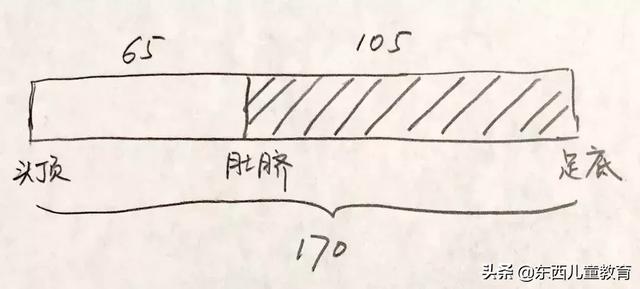
1. 用“腿長”= 105cm這個條件來算,我們假設105就是“肚臍到足底”,那麽,根據黃金分割比例:
但我們知道,實際上 “肚臍到足底” > “腿長”,所以這個人的身高就應該 > 170cm;
2. 用“頭頂到脖子下端”= 26cm這個條件來算,我們假設26就是“頭頂到咽喉”,那麽,根據黃金分割比例:
但我們知道“頭頂到咽喉”< “頭頂到脖子下端”,所以這個人的身高就應該 < 178cm。
把1和2一結合,馬上就能得出答案了,170cm < 身高 <178cm,所以該選B。
是不是挺簡單的?
解題過程中用到的畫圖建模方法,就是我們接下來要談的新加坡數學的精髓。
臨近暑假,最近很多讀者留言問到新加坡數學,都想利用暑假的時間,讓孩子系統學習下。關于新加坡數學,我在之前的分享文章、留言回複中不止一次地提到過,翻出來再次整理下,和大家分享。
先來個直觀感受,新加坡數學有多牛呢?可以說它已經是新加坡的國家名牌,受到全球家長的青睐。尤其在美國,據我了解身邊幾乎所有亞裔孩子,無一例外地刷過或正在刷新加坡數學,不少私立學校也直接選用了新加坡數學做教材。
逃逃接觸新加坡數學已經有好幾年了。他在美國上一年級時有段時間我很忙,下午放學早沒空去接,就給他找了家口碑很好的Afterschool Care(專門提供照顧孩子、輔導作業、活動安排等服務的課外培訓機構,類似于國內的托管班),每天放學會派車到學校接,然後整個下午孩子就在那裏做運動、科學小實驗和學科類的練習,其中數學他們用的就是新加坡數學的練習冊。
一開始我並沒太在意,畢竟自己在國內受過教育,當年也上過奧數,參加過競賽,後來學的也是理工科專業,別的不敢說,在數學上,多多少少有那麽一丟丟“藐視衆生”的優越感,總覺得咱們國內的數學已經很牛了,其他國家估計難出其右吧。
1、新加坡數學很善于“教”,因爲它有個利器——建模
但很快我發現,我們的數學是挺牛,但新加坡數學在“教”的層面上更爲出色。就像我們評價一位老師好不好,最關鍵的是看他會不會教,是否能讓孩子迅速搞懂並且深刻理解。
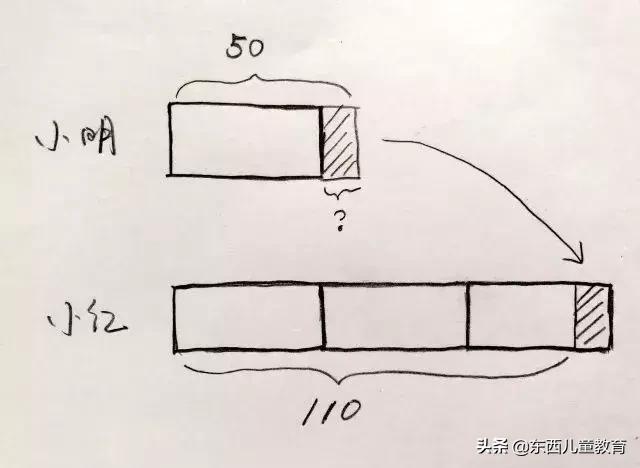
有次飯桌上我和逃爸聊起現在國內的幼升小考試有多瘋狂,順便也借用了一道“真題”考考逃逃,題目大意是“小明有50塊錢,小紅有110塊錢,問小明給小紅多少錢,小紅的錢正好是小明的3倍?”對當時沒接觸過這類題目,也還沒學過除法的逃逃來說,我們並不期望他能答出來,只是想讓他感受一下國內孩子學習的壓力,讓他知道山外有山人外有人而已。結果他的確也沒答出來,但拿了張紙畫了個圖,原稿找不到了,我來重現一下,他大概是這麽畫的:
接著給我們解釋,陰影部分的錢從小明那補到小紅這裏之後,那麽他們倆所有的錢可以分成4個一樣多的白方框,50+110是160,160分成一樣多的四份……我們告訴他每份是40後,他很快就得出了最終答案。
有點兒小欣喜,盡管當時的逃逃被計算問題擋住,但思路挺靠譜,對問題的理解,對數學的感覺也是有了的,問他怎麽想到這樣畫圖,他說不知道呢,反正就該是這樣啊。後來我翻看了他在Afterschool Care托管班做的練習題,發現這種用方框圖表達思路的方式其實就來源于他平時每天下午做的新加坡數學練習題。
看起來並不高深吧?但這恰恰是新加坡數學最牛的地方——Model Drawing,中文通常翻譯成“建模”。提到建模,估計不少學霸家長馬上會聯想到自己中學或大學時代聽說過,或參加過的數學建模競賽,其要求是用數學模型來描述解決現實世界的問題,是一個非常複雜的存在。
當然這裏所說的Model Drawing沒那麽複雜,但“建模”的思想是類似的,都是想辦法用固定的、規整的模型(比如上面的方框圖)來描述一個現實問題,這樣,對現實問題的思考就轉化成對這個模型的研究。
比如上面的這道應用題中, 130,52這兩個數量是重要的,它們之間的關系也是重要的,所以應該直接體現在“模型”裏,而其他的信息,比如那位小女孩是不是叫Jolene,她和哥哥/弟弟交換的是不是郵票,這些對解決方案沒什麽用,就不需要在“模型”中出現了。
這個方法能幫助孩子簡化問題、整理思路,也排除無用的幹擾。
2、從最簡單的加減乘除開始“建模”
新加坡數學,就是從最簡單的加減乘除開始,循序漸進地在它的教學和練習中幫助孩子Get到建模的方法和思想,讓孩子養成用圖表的形式把問題展現出來,然後再基于圖表解決問題的習慣。
Model Drawing建模最常用的方法就是畫方框,我從新加坡數學的官網上摘取了一些例子:
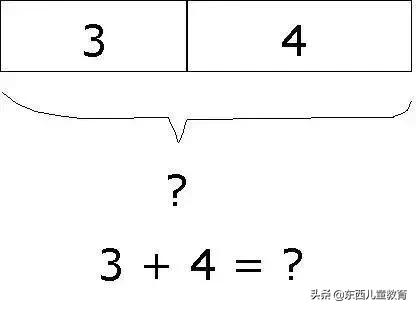
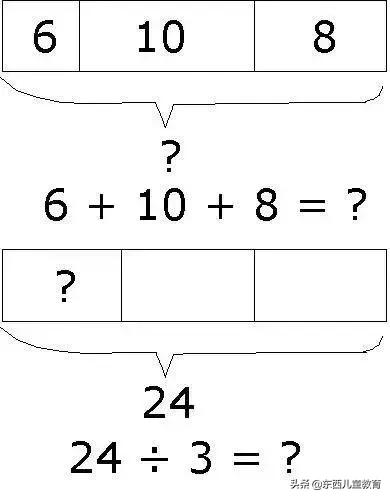
用建模學加法:
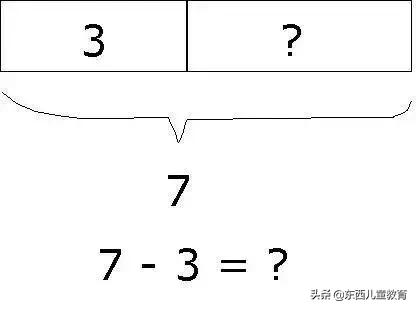
用建模學減法:
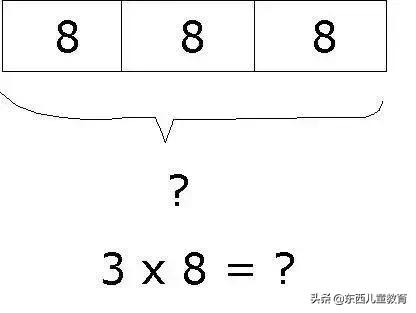
用建模學乘法:
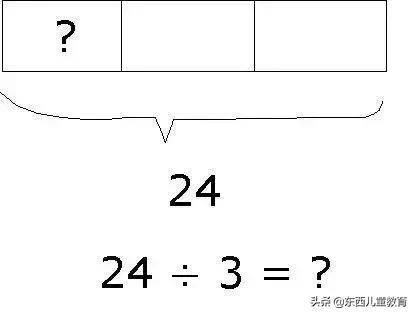
用建模學除法:
用建模學分數:
用建模學“小數”:
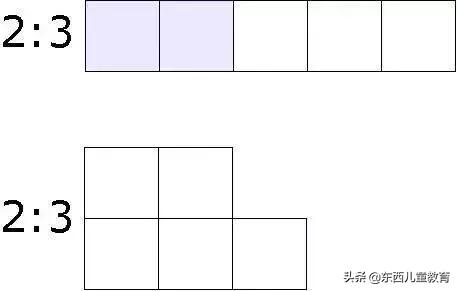
用建模理解“比例”:
用建模理解“平均數”:
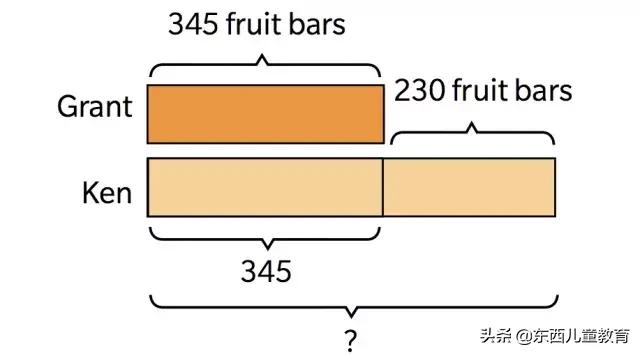
用建模解應用題:
Grant 有345個水果派,Ken比Grant多230個,問Ken有多少個水果派?
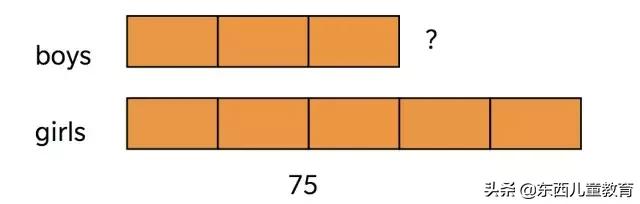
三年級有75位女生,男生數量是女生的3/5,問有多少位男生?
3、建模——數學界的“思維導圖”
方法很簡單,其實就一個關鍵點,用不同長度的方框表示數量,畫的時候盡量符合比例,這樣孩子在畫圖的過程中,對數量的大小,數量之間的關系就會有很直觀的感受。
很多孩子覺得數學困難,往往是因爲從具體到抽象這關過不好,剛開始數學啓蒙時可以掰手指,數積木塊,這時的數學是具象的,有趣的,在生活中可見的。但後面一上到抽象的數字符號,運算公式時,數學就變成一門看不見摸不著的學科了,不適應的孩子很容易産生畏懼心理。
類似于思維導圖能把我們的思考展示出來,可視化、直觀化一樣,建模可以幫助孩子把數學可視化,把抽象的數學關系轉化成看得見摸得著,也很容易用來和別人討論交流的東西,可以說是連接數學從具體到抽象之間的橋梁。
課堂上的新加坡數學
4、輔導孩子使用的小貼士
從逃逃和我們周圍孩子的使用情況來看,建模方式對孩子的數學思維幫助非常大,主要體現在兩個地方:
① 家長用建模的方式給孩子講解數學題時,直觀具體,孩子很容易理解;同時孩子用建模的方式解題時,家長也能從孩子畫圖的過程中觀察他是否完全理解掌握了知識點,有沒盲區;
② 孩子不畏懼難題,反而會喜歡上挑戰。因爲他知道一下子想不清楚的題目,用建模的方式慢慢分解,思路就會越來越清晰,在這個過程中就很有成就感。
非常推薦給大家。上面提到的這些建模方法的例子,我想對家長來說是非常簡單的,完全可以在孩子平時做數學作業時輔導引導他使用,有幾個需要注意的地方:
① 堅持使用,因爲它是培養孩子的一種思維模式,需要不斷練習讓孩子形成習慣,能條件反射地去使用,達到“不知道”自己知道的狀態,甚至能在沒有紙筆的時候,看到一道題目腦海裏也能浮想出清晰的圖形關系,這樣遇到複雜一點兒的數學題目才能保持思路清晰,有條不紊;
② 孩子畫圖的時候注意引導他盡量按照數量的比例來畫,這樣更直觀,也更容易提早“猜”出答案,這點有些類似我們以前做幾何題,圖畫得好畫得准確的話對解題很有幫助;
③ 建模方法可以在孩子平時做任何數學作業題時使用,不一定非得用新加坡的教材或練習冊,當然它能讓家長省點勁兒。
我整理了一份幫助家長理解學習和輔導孩子的材料,有需要的同學可以在我們平台回複“新加坡數學”即可獲得。
曾經有位讀者在留言中提到,“個人感覺新加坡數學是比較實用性,特別是畫圖解題的這套思維流程感覺和工作以後要用到的技巧很相似。但是論學霸級還是比不上中國某思培養出來的那些奧數高手”。
和工作的關聯這點我深有同感,比如建模的思想,本質上就是找尋繁雜事物的規律,簡化和標准化,這在很多工作中都需要用到,比如我之前做軟件設計時,最先的一步就是要把用戶的需求轉化成UML(Unified Modeling Language,統一建模語言)模型,在此基礎上再進行設計、編程。新加坡數學所培養的思維流程的確和工作要用到的技巧很接近。
論到學霸,我覺得可能是半斤八兩有得一拼,新加坡也是國際數學賽事上的常勝將軍,上一道網絡上流傳的新加坡五年級數學題,大家隨意感受下難度:
謝麗爾的生日是下列日期中的一個:
5 月15 日,5 月16 日,5 月19 日,
6 月17 日,6 月18 日,
7 月14 日,7 月16 日,
8 月14 日,8 月15 日,8 月17 日。
謝麗爾把月份告訴了阿爾伯特,把日期告訴了伯納德。
阿爾伯特說:“我不知道謝麗爾的生日,但我知道伯納德也不知道。”
伯納德說:“本來我不知道謝麗爾生日的,但聽完阿爾伯特的話,我就確定了。”
阿爾伯特接著說:“那麽,現在我也確定謝麗爾的生日了。”
問謝麗爾的生日是哪一天?
我覺得比咱的“維納斯身高”高考題燒腦多了~