### 1.2 分類問題:
#### 1. LogLoss:
$$
J(\theta)=-\frac{1}{m} \sum_{i=1}^{m}\left[y^{(i)} \log h_{\theta}\left(x^{(i)}\right)+\left(1-y^{(i)}\right) \log \left(1-h_{\theta}\left(x^{(i)}\right)\right)\right]
$$
**二分類**任務中常用的損失函數,在LR中,通過對似然函數取對數得到。也就是**交叉熵**損失函數。
#### 2. 指數損失函數:
$$L(y,f(x)) = \frac{1}{m} \sum_{i=1}^n{exp[-y_if(x_i)]}$$
在AdaBoost中用到的損失函數。
## 2.評價指標:
如何評估機器學習算法模型是任何項目中一個非常重要的環節。分類問題一般會選擇准確率(Accuracy)或者AUC作爲metric,回歸問題使用MSE,但這些指標並不足以評判一個模型的好壞,接下來的內容我將盡可能包括各個評價指標。上述損失函數大部分可以直接作爲評價指標來使用,上面出現過的簡單介紹。
### 2.1 回歸問題:
**1. MAE:
** 平均絕對誤差(Mean Absolute Error),範圍 $[0,+∞)$
$$
MAE=\frac{1}{n} \sum_{i=1}^{n}\left|\hat{y}_{i}-y_{i}\right|
$$
**2. MSE:
** 均方誤差(Mean Square Error),範圍 $[0,+∞)$
$$
MSE=\frac{1}{n} \sum_{i=1}^{n}\left(\hat{y}_{i}-y_{i}\right)^{2}
$$
**3. RMSE:
** 根均方誤差(Root Mean Square Error),範圍 $[0,+∞)$
$$
RMSE =\sqrt{\frac{1}{n} \sum_{i=1}^{n}\left(\hat{y}_{i}-y_{i}\right)^{2}}
$$
取均方誤差的平方根可以使得量綱一致,這對于描述和表示是有意義的。
**4. MAPE:
** 平均絕對百分比誤差(Mean Absolute Percentage Error)
$$
MAPE=\frac{100 \%}{n} \sum_{i=1}^{n}\left|\frac{\hat{y}_{i}-y_{i}}{y_{i}}\right|
$$
**注意點**:當真實值有數據等于0時,存在分母0除問題,該公式不可用!
**5. SMAPE:
** 對稱平均絕對百分比誤差(Symmetric Mean Absolute Percentage Error)
$$
SMAPE=\frac{100 \%}{n} \sum_{i=1}^{n} \frac{\left|\hat{y}_{i}-y_{i}\right|}{\left(\left|\hat{y}_{i}\right|+\left|y_{i}\right|\right) / 2}
$$
**注意點:** 真實值、預測值均等于0時,存在分母爲0,該公式不可用!
**6. R Squared:**
$$
R^{2}=1-\frac{\sum_{i}\left(\hat{y}^{(i)}-y^{(i)}\right)^{2}}{\sum_{i}\left(\bar{y}-y^{(i)}\right)^{2}}
$$
$R^2$即**決定系數(Coefficient of determination)**,被人們稱爲最好的衡量線性回歸法的指標。
如果我們使用同一個算法模型,解決不同的問題,由于不同的數據集的量綱不同,MSE、RMSE等指標不能體現此模型針對不同問題所表現的優劣,也就無法判斷模型更適合預測哪個問題。$R^2$得到的性能度量都在[0, 1]之間,可以判斷此模型更適合預測哪個問題。
**公式的理解:**
1. 分母代表baseline(平均值)的誤差,分子代表模型的預測結果産生的誤差;
2. 預測結果越大越好,$R^2$爲1說明完美擬合,$R^2$爲0說明和baseline一致;
**7. 代碼實現:**
“`python
# coding=utf-8
import numpy as np
from sklearn import metrics
# MAPE和SMAPE需要自己實現
def mape(y_true, y_pred):
return np.mean(np.abs((y_pred – y_true) / y_true)) * 100
def smape(y_true, y_pred):
return 2.0 * np.mean(np.abs(y_pred – y_true) / (np.abs(y_pred) + np.abs(y_true))) * 100
y_true = np.array([1.0, 5.0, 4.0, 3.0, 2.0, 5.0, -3.0])
y_pred = np.array([1.0, 4.5, 3.5, 5.0, 8.0, 4.5, 1.0])
# MSE
print(metrics.mean_squared_error(y_true, y_pred)) # 8.107142857142858
# RMSE
print(np.sqrt(metrics.mean_squared_error(y_true, y_pred))) # 2.847304489713536
# MAE
print(metrics.mean_absolute_error(y_true, y_pred)) # 1.9285714285714286
# MAPE
print(mape(y_true, y_pred)) # 76.07142857142858
# SMAPE
print(smape(y_true, y_pred)) # 57.76942355889724
# R Squared
print(r2_score(y_true, y_pred))
“`
### 2.2 分類問題:
#### 0. Confusion Matrix(混淆矩陣):
混淆矩陣一般不直接作爲模型的評價指標,但是他是後續多個指標的基礎。以下爲二分類的混淆矩陣,多分類的混淆矩陣和這個類似。
| |預測正例| 預測反例|
|–|–|–|
|真實正例|TP(真正例)| FN(假反例)|
|真實反例|FP(假正例)|TN(真反例)|
我們訓練模型的目的是爲了降低FP和FN。很難說什麽時候降低FP,什麽時候降低FN。基于我們不同的需求,來決定降低FP還是FN。
* **降低假負數例(FN)**:
假設在一個癌症檢測問題中,每100個人中就有5個人患有癌症。在這種情況下,即使是一個非常差的模型也可以爲我們提供95%的准確度。但是,爲了捕獲所有癌症病例,當一個人實際上沒有患癌症時,我們可能最終將其歸類爲癌症。因爲它比不識別爲癌症患者的危險要小,因爲我們可以進一步檢查。但是,錯過癌症患者將是一個巨大的錯誤,因爲不會對其進行進一步檢查。
* **降低假正例(FP)**:
假設在垃圾郵件分類任務中,垃圾郵件爲正樣本。如果我們收到一個正常的郵件,比如某個公司或學校的offer,模型卻識別爲垃圾郵件(FP),那將損失非常大。所以在這種任務中,需要盡可能降低假正例。
#### 1. Accuracy(准確率):
$$
Acc=\frac{T P+T N}{T P+T N+F P+F N}
$$
准確率也就是在所有樣本中,有多少樣本被預測正確。
當樣本類別均衡時,Accuracy是一個很好的指標。
但在樣本不平衡的情況下,産生效果較差。假設我們的訓練數據中只有2%的正樣本,98%的負樣本,那麽如果模型全部預測爲負樣本,准確率便是98%,。分類的准確率指標很高,會給我們一種模型很好的假象。
#### 2. Precision(精准率):
$$
P=\frac{T P}{T P+F P}
$$
**含義:** 預測爲正例的樣本中有多少實際爲正;
#### 3. Recall(召回率):
$$
R=\frac{T P}{T P+F N}
$$
**含義:** 實際爲正例的樣本有多少被預測爲正;
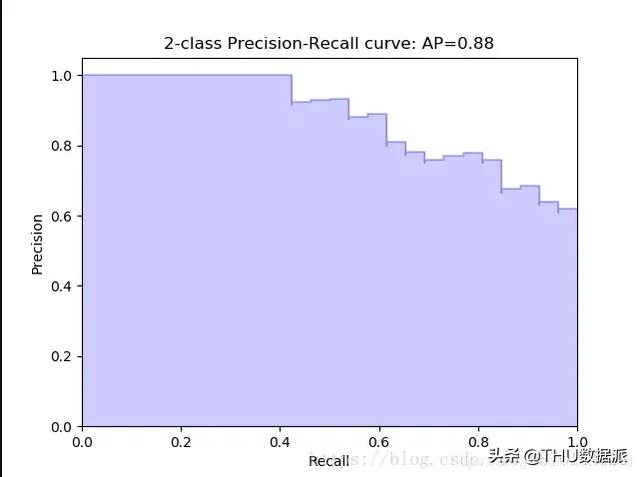
#### 4. P-R曲線:
通過選擇不同的阈值,得到Recall和Precision,以Recall爲橫坐標,Precision爲縱坐標得到的曲線圖。
**曲線性質:**
1. 阈值最大時,對應**坐標點爲(0,0)**,阈值最小時,對應**坐標點(1,1)**;
2. ROC曲線越靠近左上角,該分類器的性能越好;
3. 對角線表示一個隨機猜測分類器;
4. 若一個學習器的ROC曲線被另一個學習器的曲線完全包住,後者性能優于前者;
**AUC:** ROC曲線下的面積爲AUC值。
#### 7. 代碼實現:
“`python
from sklearn.metrics import accuracy_score,precision_score,recall_score,f1_score,fbeta_score
y_test = [1,1,1,1,0,0,1,1,1,0,0]
y_pred = [1,1,1,0,1,1,0,1,1,1,0]
print(“准確率爲:{0:%}”.format(accuracy_score(y_test, y_pred)))
print(“精確率爲:{0:%}”.format(precision_score(y_test, y_pred)))
print(“召回率爲:{0:%}”.format(recall_score(y_test, y_pred)))
print(“F1分數爲:{0:%}”.format(f1_score(y_test, y_pred)))
print(“Fbeta爲:{0:%}”.format(fbeta_score(y_test, y_pred,beta =1.2)))
“`
### 參考資料:
[1. 分類問題性能評價指標詳述]
(https://blog.csdn.net/foneone/article/details/88920256)
[2.AUC,ROC我看到的最透徹的講解]
(https://blog.csdn.net/u013385925/article/details/80385873)
[3.機器學習大牛最常用的5個回歸損失函數,你知道幾個?]
(https://www.jiqizhixin.com/articles/2018-06-21-3)
[4.機器學習-損失函數]
(https://www.csuldw.com/2016/03/26/2016-03-26-loss-function/)
[5.損失函數jupyter notebook]
(https://nbviewer.jupyter.org/github/groverpr/Machine-Learning/blob/master/notebooks/05_Loss_Functions.ipynb)
[6.L1 vs. L2 Loss function]
(http://rishy.github.io/ml/2015/07/28/l1-vs-l2-loss/)
[7. P-R曲線深入理解]
(https://blog.csdn.net/b876144622/article/details/80009867)
編輯:于騰凱
校對:林亦霖
作者簡介
董文輝,電子科技大學碩士,主要研究方向:推薦系統、自然語言處理和金融風控。希望能將算法應用在更多的行業中。
—完—
關注清華-青島數據科學研究院官方微信公衆平台“ THU數據派 ”及姊妹號“ 數據派THU ”獲取更多講座福利及優質內容。