作者 l 秦柔雲 編輯 l 粥左羅

來源 l 粥左羅的好奇心（ID：fangdushe007）

很多人經常說，我不想成爲牛人，平平淡淡就好。

你想這樣，社會不允許。

最近網絡上發生了很多事，都在告訴我們，做個普通人，是件風險很大的事，做不了牛人大咖，也要盡可能往上走，越往上，越安全。

自己變強，是解決一切的根本。

問題是，如何變強？不能只靠勤奮，996甚至007都解決不了問題，情商高一點，更聰明一點，都可以，但長期看來，人與人最大的差距，是思維模式的差距。

思維不同，看到的世界不同，做出的行動不懂，擁有的人生不同。

00

不同的思維

成就不同的人生

給大家講個故事：消失的彈孔。

哥倫比亞大學有個統計研究小組，它的任務是組織美國的統計學家爲“二戰”服務。

這個小組裏集合了美國最頂尖的數學家，他們通過各種數據，制定最合適的戰爭策略。

美國不希望自己的飛機被敵軍擊落，因此要給飛機外層加盔甲，但這裏有個矛盾：

如果盔甲覆蓋不足，就會導致防禦不足，如果盔甲過多，就會太重，影響飛機的靈活性，依然會導致防禦不足。

如何找到一個最優解呢？

軍方提供了各種相關數據，數學家們就要通過這些數據來得出結論。

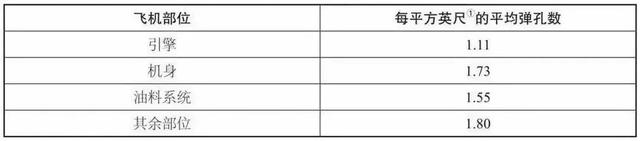
其中一個數據，是不同的飛機部位留有的彈孔的數量不一樣。

美國軍方認爲，如果不能全部加盔甲，那麽盔甲就應該加在飛機受攻擊概率最高的地方。

這不是廢話麽？當時應該這樣。

不對，這是固有的思維方式，只關注看得見的東西。

頂級優秀的人，會怎麽思考？

數學天才瓦爾德給出了完全不同的答案：盔甲應該加在沒有彈孔的地方，也就是飛機的引擎。

瓦爾德關注看不見的東西：

飛機各個部位受到攻擊的可能性是均等的，爲什麽在引擎上留有的彈孔數量卻遠遠少于其他的部位呢？消失的彈孔又到哪裏去了呢？

瓦爾德猜測，這些消失的彈孔都在未能返航的飛機上。

大量的飛機在機身被打的千瘡百孔的時候仍然能夠返航，可一旦引擎，受損飛機可能就回不來了。

軍隊醫院病房裏，腿部受傷的病人，比胸部中彈的病人要多得多。這顯然不是因爲腿部更容易中彈，而是因爲胸部中彈的人都死了。

美軍采用了瓦爾德的建議。

我們很難說瓦爾德究竟挽救了多少美軍戰機，但是根據美國國防部的研究發現，如果飛機被擊落的概率比敵軍少5%，耗油的概率少5%，步兵供給多5%，成本比對方低5%，往往就會成爲勝利方。

你看，同一件事，思維模式不同的人，看到的東西截然不同，采取的行動也會截然不同。

巴菲特的合夥人查理芒格，是一個靠智慧取勝的典型，他一生信奉並踐行多維思維模型。

是的，思維模型有很多，但一篇文章講不了所有，我們今天給大家講其中一個最重要的思維模型：

數學思維。

幾乎每個人都學過數學，厭惡數學，認爲數學不過是考試工具，畢業了就沒用了。但這篇要告訴你，數學才是最頂級的思維模型。文章把數學思維中對個人誠成長幫助最大的5個思維分享給大家。

不要擔心，本文講的數學思維，你都看得懂，看完一定會有很大收獲。

01

做什麽不做什麽？

概率思維告訴你

無論是這一生，還是職業生涯中，我們面臨的問題，都可以歸結爲三個：要做什麽？不要做什麽？要重複做什麽？

如果你有概率思維，這事兒就好解決了。

比如結婚這種人生大事，很多人一拖再拖還拖，總是說：我還沒有找到我一生中的唯一最愛，我甯願不結婚！

給你講個真事。

一個男孩給叔叔寫信說：我要爲女朋友放棄事業，跟女朋友到另外一個城市去，因爲這個女朋友是我一生中唯一最愛。

叔叔寬容的一笑說：當然你可以做自己的決定，但如果你真的認爲這女孩是你一生唯一最愛的話，那我告訴你，世界上兩個唯一最愛的人，相遇的機會是零。茫茫人海，你們在有限的生命裏不可能遇見對方。

男孩的叔叔是大經濟學家弗裏德曼，他是在用概率思維看問題。

概率思維會告訴你：在70億顆綠豆中放上兩個紅豆，不斷的去攪拌它們，就算花上一生的時間，這兩個紅豆也幾乎無法相遇。

所以，找對象這件事，根本不存在找到唯一的最愛，而是在你身邊接觸到的人裏找個最匹配解決方案。

聽起來不浪漫，但其實大家都是這麽做的。

概率思維告訴你：不要做概率幾乎爲零的事，多做大概率能做成的事。

哪些事要重複做？

你要重複做一件事，肯定想變成一個值錢的人。

我先給你講一個值錢的花瓶。

何書元編著的《概率論》中，有一道關于青瓷花瓶的題：

明永樂年間的“青花如意垂肩折枝花果紋梅瓶”非常值錢，價值1.6866億港元。

稀缺是值錢的重要原因之一，我們假設一只青瓷花瓶在一年內被失手打破的概率是3%，如果明朝正德年間生産了10000只青花瓶，請問現在還剩多少個？

計算方法如下：

第一步、先計算一只青花瓶500年保持完好的概率：

P = （1-0.03）的500次方

答案預計是2.43乘以10的負7次方。

你可能看不懂這個公式，但你能明白答案告訴你，概率非常非常非常低。

第二步、計算1萬只花瓶保持完好的概率：

0.00243

什麽意思？

我們還能見到該花瓶的概率是0.243％。

我們把這個過程稱爲“概率的複利”。

概率的複利該怎麽用呢？

我們把事情分爲三種收益模型：

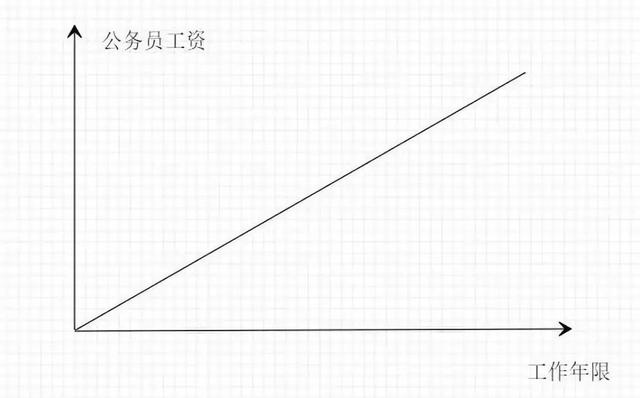
第一、等比例線性增長收益模型：

比如做公務員，收入變化不大，收益幾乎是等比例增長，一個月賺5000，一年賺6萬。

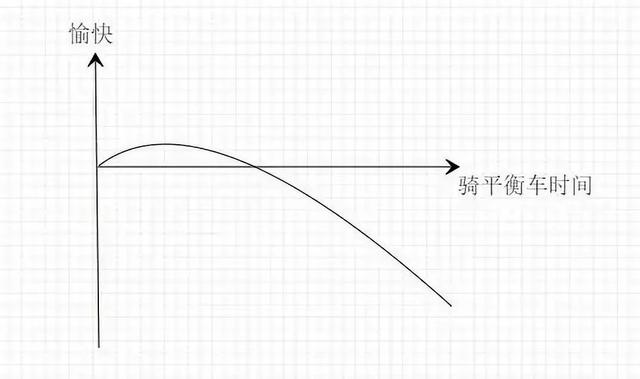
第二、上行回報有限下行損失無限的收益模型：

今日頭條的張一鳴發過一條朋友圈：准備把同事的平衡車給沒收了，工程師騎平衡車通勤簡直是置公司重要資産于風險之中。

騎平衡車上下班就是上行回報有限下行損失無限的典型，騎上去的時候，速度快，又方便，感覺很爽，然後好處就這些了，剩下的就是一旦出事，付出的代價就是無法承受的。

普通人的思維是看當下，頂級優秀的人通過概率思維會判定：只要把時間拉到足夠長，你擔心的事情一定會發生。

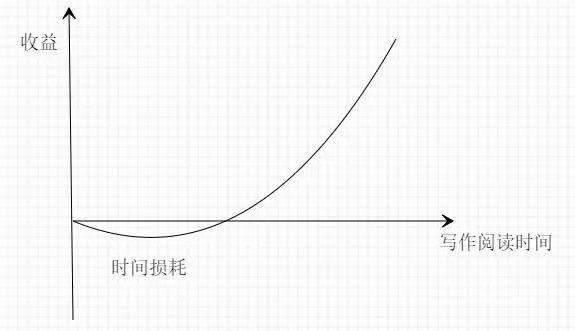
第三、下行損失有限上行回報無限的收益模型：

我們下班讀書，業余的時間寫作，就是這樣，我們損失的就是閑暇的時間，然後長期堅持，獲得的收益是無上限的。

當年蔡崇信放棄了580萬年薪，加入阿裏跟馬雲一起創業，一個月拿500塊。

這怎麽理解呢？

蔡崇信說：耶魯法學院的學位是這世上少見的珍寶，在政府和商業世界裏都很稀缺。換句話說，我去冒險，風險收益是不對稱的，下行風險很小，上行收益可能很大。說到底，如果我去阿裏巴巴幹半年，公司不行了，我還是可以再回頭去幹稅務律師或者做投資。

這樣的事情，就是時間的朋友，雖然單個事件看起來概率非常小，但隨著時間積累，成功的概率會越來越大，這就是概率的複利思維。

知道了概率，我們就明白了，有些事可以做，有些事不能做，而重要的事情需要長期做。

02

如何加速個人成長？

微積分思維告訴你

讀過高中的，都學過微積分，曾經我已經那只是考試用得上，現在我明白，微積分是一種思維模型，不懂微積分，思維方式會不同，眼中的世界也會有差別。

去年羅輯思維帶火了一個詞：

小趨勢。

比起普通人無法把控的大趨勢，真正能給所有人帶來機會，從細微處引發大變化的，恰恰是我們身邊的各種小趨勢。

小趨勢，是影響趨勢的趨勢，帶來改變的改變。

這不就是微積分中的“微分”麽？

微分思維，就是從宏觀趨勢中，把握每個細節變化，在大量不確定性或者說大量變量中，認清每一步，找到前進的方向。

微分思維是從宏觀中看微觀，積分思維是從微觀看宏觀變化。

積分是一個從瞬間到連續的過程，事物平緩的變化著，如果把曲線看成一個一個的點，每一個瞬間看起來都是與上一個瞬間相連的，然而積累之後，卻早已和原來差距十萬八千裏了。

其核心假設是：事物都在平緩地發生變化，任何事物都與其此前的一刻有著無限小的差異。

亞馬遜的CEO問過巴菲特一個問題：

你的投資理念非常簡單，別人爲什麽不複制你的做法？

巴菲特回答：因爲大多數人不願意慢慢變富。

拾遺君曾經講過一個高中同學的故事。

高中同學打算做個公衆號，寫了一段時間，沒有進展，他以爲是自己不懂爆文的原理，買了很多《如何寫出10W+》，《從零開始做公衆號月入10萬》之類的課程。

堅持了幾個月，效果還是不好。

他想著也許是自己營銷能力不足，又開始學《營銷入門》….還是不行，他又開始學….

結果折騰三年，公衆號還是沒做起來。

如果僅僅關注在一個點上，我們看到的全是細枝末節，拉長曲線，才能聚焦到真正的重點上。

這是因爲，我們此時此刻的生活，仿佛是微積分曲線中的一個點，普通人只能看到那一個點，因此我們就會很著急，我們不願意慢慢變富，不願意一點點接近目標，而總想著要走捷徑。

懂微積分的人，會從微分的角度看那一點代表的小趨勢，會從積分的角度去看發展的威力。

吳軍老師說，不要太在乎你的第一份工作的薪水。

生涯規劃師古典也說，年輕人入職前7年，不要太在意情感回報，而是要聚焦在能力的提升上。

這就是用微積分思維看個人成長。

有微積分思維的人，會自動的離問題遠一些，不僅盯著當時的瞬間，也看見人生的曲線，從何處來又去向何方，你尋本溯源，找到問題真正的關鍵節點。

03

什麽從根本上決定一個人的命運？

幾何公理思維

有一個嚴密的邏輯體系，叫幾何學。

幾何學怎麽來的？

上過學的我們，都知道兩個詞，公理和定理。

兩者有何區別？

比如著名的勾股定理，勾三股四玄五，這就是定理，定理是由公理推出來的。

公理就是公認的道理，是人類理性的不證自明的基本事實，經過人類長期反複實踐的考驗，不需要再加證明的基本命題。

咱們學的幾何學，叫做歐式幾何。

古希臘大數學家歐幾裏德寫的《幾何原本》裏，系統地總結了古代勞動人民和學者們在實踐和思考中獲得的幾何知識，他把人們公認的一些事實列成定義和公理，以形式邏輯的方法，用這些定義和公理來研究各種幾何圖形的性質，從而建立了一套從公理出發，論證命題得到定理得幾何學論證方法，形成了一個嚴密的邏輯體系——歐式幾何學。

歐式幾何學就是從五大幾何公理基礎上來的：

三角形內角和180度。

兩點確定一條直線。

兩條平行線永不相交。

所有直角都全等。

任何線段，可以以其中一個斷點爲圓心，該線段爲半徑做一個圓。

根據這5個幾何公理，我們可以推出一整個幾何體系，而體系中各個定理一定邏輯自洽。

從虛無中創立大廈，公理是最底層邏輯。

幾何公理思維就是：一切都有最底層的邏輯，它對整個大廈起到根基性的作用，如果根基不好，大廈又怎能屹立？

決定一個人一生命運最根基性最底層的邏輯是什麽？

價值觀。

我們常常說一個人“不理智”，指的就是底層“公理”——價值觀，互相矛盾。

很多人覺得價值觀不重要，虛頭巴腦的。

果真如此嗎？

2001年的阿裏正處于生死存亡之間，錢已經燒完，盈利還看不到，下一筆融資還不知道在哪裏。

也是在這個時候，關明生走進了阿裏。

大家都等著這位才子大展身手，但關明生拉著馬雲幹了件奇怪的事情：定價值觀。

關明生問馬雲：你想要一個什麽樣的公司？

而馬雲居然很認真的開始想這個問題，拉著人一起討論。6個人花了7個小時，搞出了一個價值觀雛形——獨孤九劍。

很多人不看好，覺得公司最重要的是能賺錢，價值觀能拉來業績嗎？

但馬雲對待價值觀是認真的。

他根據價值觀考核，甯可要一個價值觀好，但能力欠缺的“小白兔”，也不要能力強，沒有價值觀的“野狗”。

甚至因爲違反了價值觀，他還開除了業績最好的員工，馬雲是瘋了嗎？

關明生說：價值觀是我們的DNA，管轄著我們的行爲，能夠産生凝聚力。

阿裏發展至今，不得不說是因爲堅定的價值觀，産生了強大的作用力，員工們互相幫助，以自己是阿裏人爲傲。

作爲個人也是一樣，一個人的價值觀，其實就是一個人的行爲准則，混亂的價值觀必然導致混亂的人生，從根本上決定一個人能做出什麽樣事的，是他的價值觀。

04

如何在複雜的世界中

不被歸因錯誤所迷惑？

代數思維告訴你

上小學的時候，我們遇見了數，學會了數的加減乘除。

我們可以用簡單的數來理解這個世界了。

比如，5大于3。

那麽學習5個小時的人，就比學習3個小時更厲害麽？

顯然不是，這是單一歸因，我們的世界遠遠比這個複雜。

學習的效果，不僅僅取決于學習的時長，還有目標是否明確，方法是否合理。

假設學習效果Y，它肯定和很多因素有關，比如時長（A1），目標（A2），方法（A3）之間，有著線性關系。

這樣就形成了最基本的線形代數。

Y = ｛A1，A2，A3｝

有了代數思維有什麽好處呢？

先講個大家都聽說過的實驗，著名的棉花糖實驗。

棉花糖實驗，一直被大衆誤讀：

實驗者放一個棉花糖在桌子上，叫4歲的小孩子坐在桌邊，告訴他們：

如果他們能堅持20分鍾不吃，那麽實驗員會再獎勵他們一顆。

如果他們吃掉棉花糖，就什麽也得不到。

實驗的初衷是爲了研究孩子如何抵抗誘惑。

可是設計者無意在幾年後發現，實驗結果和孩子的學業表現高度相關。

在這之後，很多家長在重複這個實驗，甚至有機構用實驗來測試孩子的未來成就。

有了代數思維後，我們知道事物之間的關系是非常複雜的，有時候兩者之間並非是線性關系，有時候就算有線性關系，也並非因果。

比如上面提到的棉花糖實驗，研究員同時也發現：

實驗結果和家庭收入也成正相關。

什麽意思呢？

也就是說家庭比較富裕的孩子，在棉花糖實驗中表現的更好。

這其中的因素就有很多。

比如我們可以假設家庭富裕的孩子，因爲平時經常接觸各種誘惑，所以對棉花糖抵抗力強。

實驗結果因此有了不同的解讀，是孩子有毅力，所以成績好呢？還是因爲孩子的家庭富裕，所以父母可以提供更多的資源，導致成績好呢？

當然我並非說毅力不重要，而是很多家長，還有早教機構用類似方法來測試孩子，預言孩子未來的學業成就，這是件很傻的事情。

和小學時候學習的簡單數學不一樣，代數並不說明結果，而只是在意事物之間的複雜關系。

擁有代數思維的人不會簡單的把兩個事物因果相連，錯誤的歸因必然導致錯誤的結論。

現實世界中，歸因錯誤是很大的一個思維誤區，代數思維最直接的會告訴我們，不要單一歸因，要複雜歸因。有了代數思維，我們就不會輕易被虛假的因果關系忽悠了，而是多維度的看問題。

05

我可以在職場中持續獲得超額收益麽？

博弈論思維告訴你

先給大家講一個新加坡大罷工的故事。

有一次，新加坡航空的機師鬧起了罷工，集體要求漲薪30%，新加坡航空的航線癱瘓了。

新加坡總理李光耀在講話中憤怒的說：

新加坡是我一手建立起來的國家，只要我還在管理，就不允許任何人破壞它！給你們一個小時想清楚，要麽回去上班，要麽走人，我可以明天就讓新航恢複正常。

超級霸氣！

最後的結果，自然是罷工的員工乖乖回去上班了。

爲什麽罷工並不能漲工資呢？

現實職場中，可能也有人偶爾閃現出這樣的念頭：咱們員工能不能共同施壓，要求老板漲工資呢？

因爲工資其實是各個公司的老板和員工們博弈的結果。

這就是雙向博弈，一共三種情況：

01 如果一個普通程序員找老板要漲薪30%，會怎樣？

老板會想，一顆普通的大白菜5毛錢，這個白菜也就那樣，還要1塊錢一顆，算了，不買了。

02 那如果公司裏，所有的程序員集合起來，要求老板漲薪30%呢？

那可能出現兩種情況：

第一種：因爲員工漲薪30%，所以成本上升，售價上升，被別的更便宜的公司踩下去，倒閉，所有人失業。

第二種：老板一看，成本上升太多，不賺錢了，算了，關門大吉，所有人失業。

01 那如果全世界的程序員都要求漲薪30%呢？

必定會有大量的大學生選擇讀計算機，土木，機械，電子，財務拼了命轉行，最後拉低平均收益。

超額收益是不可維持的。

因爲所有的收益都一定是博弈後的結果。

那麽，如何提高自己的收益呢？

薛兆豐老師說過，最好的策略是要別人不要996，自己卻996。

什麽意思呢？

其實，員工和員工是競爭關系，老板和老板是競爭關系，員工和老板不競爭。

簡單的說，老板一定會選擇性價比最高的員工，對吧，就像你去超市購物，一定貨比三家，選性價比最高的。而員工呢？一定會選擇能力範圍內待遇最好的老板。

看看你的周圍，對的，決定你收益的不是老板，而是你身邊的同事們。想獲得更高的收益，必然需要更少的競爭者。

進窄門，走遠路，見微光。你需要做別人不敢做，不願做，不能做的事情。

以上就是對你終身有用的5個思維，希望你可以時常用它們來指導你的行動。

同一件事，思維模式不同的人做，效果就會截然不同。有時候，你暫時的落後，不是你智商低，不是你情商低，而是你在思維模型上出了問題，改變你的思維，升級你的思維，你的世界就不同，你的人生就不同。

劉潤老師說過一句話：

普通人改變結果，優秀的人改變原因，而頂級優秀的人改變模型。

希望你擁有好的思維模型，成爲一個更優秀的自己。

（此處已添加圈子卡片，請到今日頭條客戶端查看）

本文來源：公衆號 @粥左羅的好奇心，作者秦柔雲。

TO BE, TO UP，這裏是50萬年輕人的成長充電站。運營者粥左羅，90後，畢業四年從服裝店員做到成功創業，從月薪2300到月入20萬，堅信成長即財富，只寫最接地氣的成長幹貨。